The blue eyes island is a tricky logic puzzle that has several variations. The one I was first told was:
A group of people live in an island with no contact with the outside world.
Eyes color is big taboo for them and they strictly follow this rule: if anybody figures out the color of their own eyes, they will commit suicide the following night.
Everybody knows the eyes color of all the other islanders, but nobody knows their own eyes color.
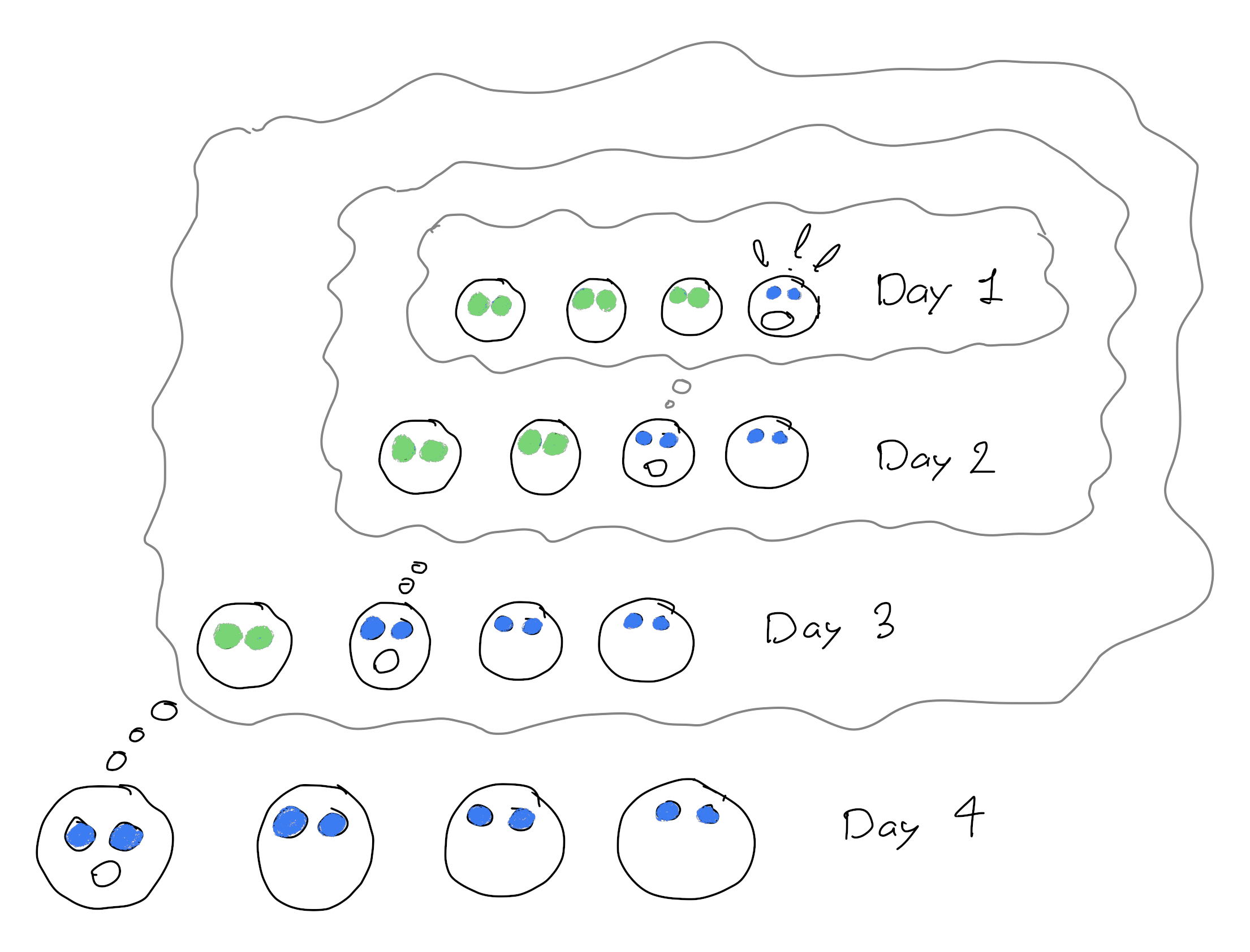
The island has 100 people with blue eyes, and 100 with green eyes. We also assume that they are all perfect logicians (and they all know that), and that they can all see each other.
One day, a stranger comes into the island and tell them:
“I can see someone with blue eyes”
What happens the following days?
If you don’t know the answer yet it would be worth stopping here for a while.
There is a simple recursive solution: if we call N the number of islanders with blue eyes, it’s clear that for N = 1, the single islander will suicide on the first day. So the proposition is that for N blue eyed islanders, we have N suicides on day N (counting from the arrival of the stranger). This is true for N = 1.
If the proposition is true for N, then we can show it to be true for N + 1, like this:
At day N, each blue eyed islander will make this reasoning:
“There is either N, either N - 1 blue eyed islanders (depending on my own eyes being blue or not). If there was N - 1 blue eyed islander, yesterday at day N - 1, there should have been N - 1 suicides. Since there was none, it means that there can only be N blue eyed islanders, which means that my eyes are blue, so I must suicide tonight”.
So the proposition is recursively true, and for N = 100, we have all the blue eyed people committing suicide on day 100.
An other way to think about the problem is to say that, being perfect logician, each islander will consider both case “I have blue eyes” or “I don’t have blue eyes”, and check for inconsistency with the observed world, assuming all the other islander do the same process."
This can be put into a python program (I use a simpler case of 5 blue eyed and 5 green eyed islanders because the complexity explodes quickly with larger numbers):
#!/usr/bin/python3
N = 5 # Number of blue eyed islanders.
M = 5 # Number of green eyed islanders (does not affect the result).
class World:
'''Define a state of the island'''
def __init__(self):
self.day = 1
self.eye_colors = ['b'] * N + ['g'] * M
self.alives = [True] * N
def copy(self):
'''Make a copy of this world'''
world = World()
world.day = self.day
world.eye_colors = self.eye_colors[:]
world.alives = self.alives[:]
return world
def set_eye_color(self, idx, color):
'''Set the eye color of a villager'''
self.eye_colors[idx] = color
return self
def yesterday(self):
'''Return a copy of the world at day - 1'''
world = self.copy()
world.day -= 1
return world
def is_world_possible(world):
'''Test whether a world is self consistent'''
# Need at least one blue eye.
if not any(x == 'b' for x in world.eye_colors): return False
# None of the alive people knew his eyes color the day before.
if world.day > 0:
yesterday = world.yesterday()
for idx, alive in enumerate(world.alives):
if know_his_eyes_color(yesterday, idx) == alive:
return False
return True
def know_his_eyes_color(world, idx):
'''Test if a islander knows his eyes color in a given world config'''
worlds = [world.copy().set_eye_color(idx, 'b'),
world.copy().set_eye_color(idx, 'g')]
return len([x for x in worlds if is_world_possible(x)]) == 1
# Initial state at day zero.
world = World()
day = 0
while True:
day += 1
print(f'Day {day}')
world.day = day
yesterday = world.yesterday()
for idx, alive in enumerate(world.alives):
if know_his_eyes_color(yesterday, idx):
print(f'Islander {idx} committed suicide')
world.alives[idx] = False
world.eye_colors[idx] = ''
if not any(x == 'b' for x in world.eye_colors):
print('No more blue eyed islanders')
break
The output of this program gives the answer for the N = 5 case:
> python3 ./blue_eyes.py
Day 1
Day 2
Day 3
Day 4
Day 5
Islander 0 committed suicide
Islander 1 committed suicide
Islander 2 committed suicide
Islander 3 committed suicide
Islander 4 committed suicide
No more blue eyed islanders
We can easily adjust the code for more complicated cases (what happens if the stranger kills a islander during the night, etc.).