This famous puzzle goes like this:
Two bicycles are traveling toward each other at the same speed until they collide; Meanwhile a fly is traveling back and forth between them, also at a constant speed. The bicycles start 20 miles apart, and travel at 10 miles per hour, and the fly travels at 15 miles per hour. How far does the fly travel in total?

If you don’t know this puzzle I suggest that you stop and think a bit about it, see if you can solve it.
The trick is to notice that the bicycles will collide after exactly one hour, and since the fly travels at constant speed of 15 miles per hour it will have traveled exactly 15 miles.
According to the story, when John von Neumann was told of this puzzle by Max Born, he immediately gave the correct answer. Max Born then remarked than most other people he told the riddle didn’t see the trick and instead tried to sum all the segments of the fly path. Von Neumann then replied that he also didn’t see the trick and in fact did compute the infinite sum.
When I heard of this story it got me wondered what though process exactly did von Neumann follow? Can the problem actually be solved that way, even by a genius? So I though a bit about it, avoiding using pen or paper, and after much effort I was also able to solve the problem the hard way (of course it helped that I already knew the answer).
The problem can be visualized as a space time diagram, with time as the vertical axis, and position as horizontal axis. It looks like this:
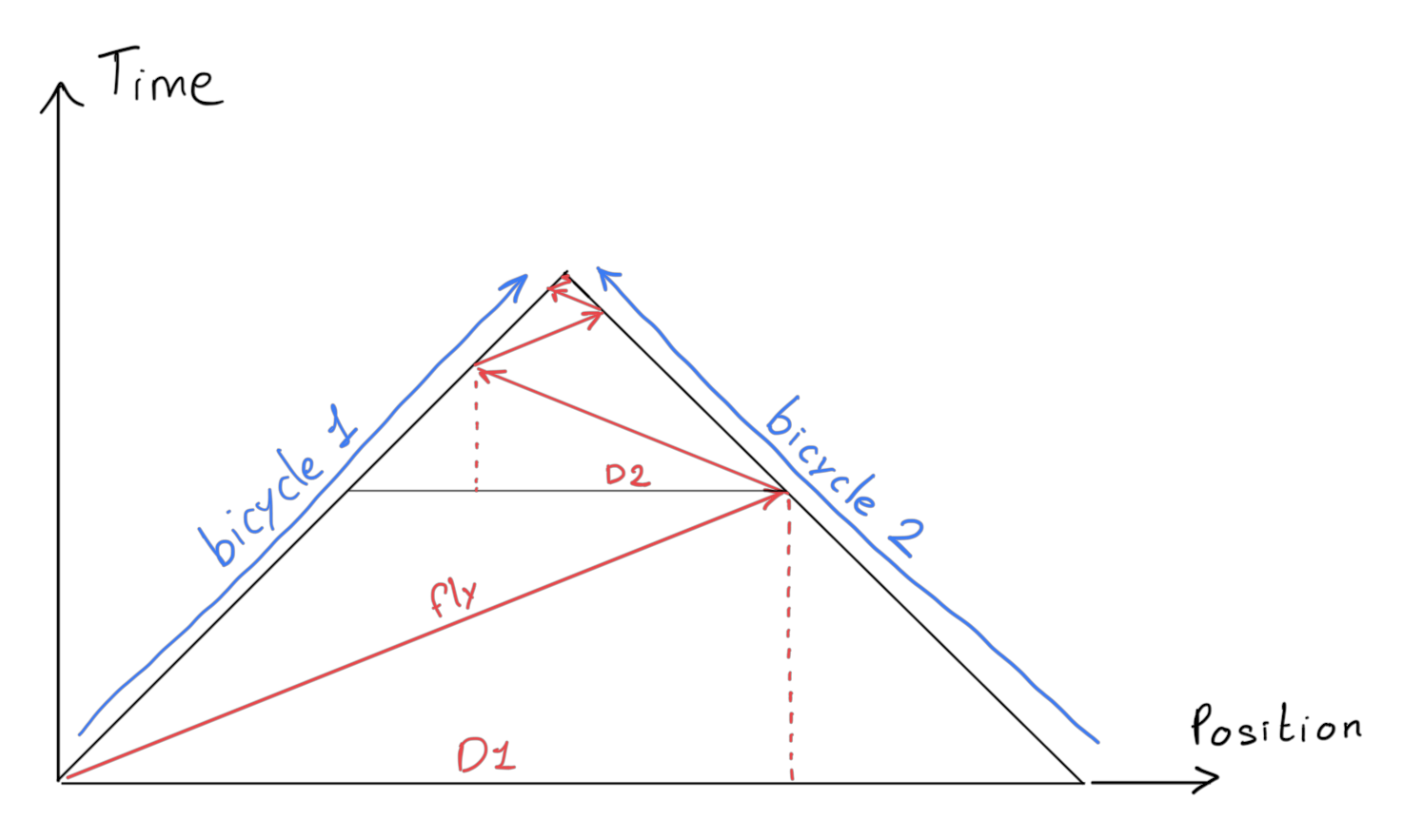
Immediately we can guess that the solution will be an infinite geometrical sum, because each segment of the fly is similar to the previous one, with only a constant scale factor applied. That is, the image is a kind of fractal: if you flip the big triangle and shrink it, it can overlap exactly with the second stage triangle. So each segment traveled by the fly is a constant time the previous segment:
$$ D_{n+1} = R D_n $$
Once we are convinced of this, all we have to do it compute:
- The distance of the first segment: $D_1$
- The ratio between consecutive triangles: $R$.
Then the solution will be the infinite sum:
$$ D_{tot} = D_1 + D_1 R + D_1 R^2 + D_1 R^3 … $$
That we know is equal to:
$$ D_{tot} = D_1 \frac{1}{1 - R} $$
All we have to do now is compute $D_1$ and $R$.
Once again we can stop and compare ourself with von Neumann by trying to do all that in our head, see if we can do it.
One way is to pose and solve the equations:
$$ \begin{align} T_1 S_{fly} + T_1 S_{bicycle} = D_1 \\ L_1 = L - 2 (L - D_1) \\ R = L_1 / L \end{align} $$
Maybe von Neumann did it like that, but for mortal like us, we can also use the fact that the ratio of the speed of the fly to the speed of the bicycles is 3 to 2. So if we redraw the first part of the triangle using a unit distance that splits the base length into 5 parts, we get something like that:
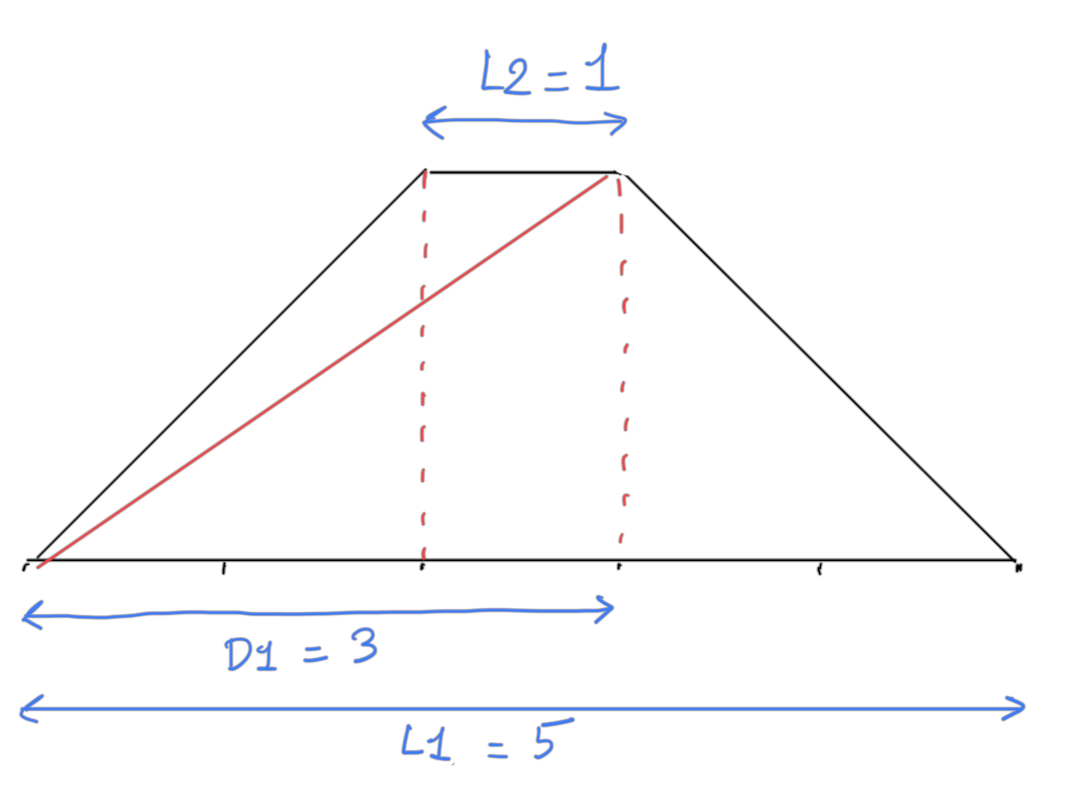
From this image we immediately see that the ratio of our geometric series will be $R = \frac{1}{5}$, and the first segment length is $D_1 = 20 \times \frac{3}{5} = 12$
Finally we substitute the values in the geometric sum formula to get the final result:
$$ D_{tot} = 12 \times (1 - \frac{1}{5}) = 12 \times \frac{5}{4} = 15. $$
And that’s all there is to it. Not too difficult with a pen and paper, and with some effort doable without. Of course only a genius like von Neumann would be able to do all that in an instant.